
The Dubi Group
Department of Chemistry
Ben-Gurion University of the Negev
Link to a movie which summarizes my research
Energy transport in nanoscale junctions
Thermoelectric energy conversion in nano-scale junctions: Thermoelectricity is the conversion of a Temperature difference into electric power. It is extremely useful in situations in which there is a large temperature difference or in which ease of maintenance is important and for waste heat recovery. Unfortunately, state-of-the-art thermoelectric systems suffer from poor efficiency and high costs, making them poor competitors to standard energy conversion methods and useful only for niche applications.
We examine theoretically the potential of using novel nano-scale junctions as thermoelectric elements. Examples include single-molecule junctions (circuits composed of a single molecule attached to two metallic electrodes, schematically depicted in Fig. 1a), junctions with a monolayer of molecules (Fig. 1b), nano-particle junctions, where a nano-particle – an ordered cluster of atoms – is placed between electrodes (Fig. 1c), and hybrid junctions containing combinations of the above (Fig. 1d).
Energy transport in photosynthetic complexes
Photosynthesis is one of the most elementary processes on this planet and a key element in the development of life on Earth. Amazingly, photosynthetic (PS) complexes – molecular structures in which photosynthesis occurs in plants and algae – have remained unchanged for millions of years, implying that they are, at least in some sense, optimally adjusted to their functionality.
The central region of PS complexes is a network of large molecules on which electronic excitations (excitons) travel from the antenna (where they absorb energy from the sun) to the reaction center (where that energy is transformed into chemical energy), as is depicted in Fig. 3. The efficiency of the PS process is largely determined by the efficiency at which excitons travel from the antenna to the reaction center.
Recently an amazing discovery was made: it was demonstrated experimentally that despite the “dirty” environment of the PS complexes, excitons maintain their coherent quantum nature, and it was shown theoretically that quantum coherence can shorten the travel time of excitons in the PS network. The premise is that this “quantum speed-up” is good for the efficiency of the energy transfer process from the antenna to the reaction center, making this the first example of direct quantum effects in biological systems. However, this idea remains a premise—calculating the energy transfer efficiency is problematic and relating it to the quantum nature of the excitons is even more problematic. Theoretical calculations to date do not address efficiency directly, but only exciton dynamics in a closed system, without treating the antenna or the reaction center directly.
We study how the efficiency of the excitonic energy transfer is affected by various elements in the PS complex, including network geometry, electronic properties, connectivity, environment properties, memory effects, etc. As opposed to other groups that treat the isolated dynamics of the PS complex, the approach we take is that of an open system – using the method we have developed for the study of molecular photocells. Thus, we can calculate quantities, such as energy currents and exciton currents, which are beyond the capability of other groups.
Heat flow in complex low-dimensional systems
All the above examples address, in some form or another, the flow of electrons and the energy transfer related to that flow. However, there is a large class of systems that are electronically inactive but allow energy to flow in the form of molecular vibrations. Central examples are insulating polymers, specifically DNA, the well-known “molecule of life”. With collaborators from Los-Alamos National Laboratory, I have been studying the heat transport properties of DNA nanoscale junctions. Using simplified DNA models that map the DNA molecule into a set of balls connected with non-linear springs (Fig. 4), we have shown that due to the unique structure of DNA – and specifically its tendency to undergo denaturation at high temperatures – it can be used as a “thermal switch” (a theoretical prediction that was verified experimentally!).
This topic is interesting for two main reasons. The first is that it has the potential to lead to the development of novel devices for the control and manipulation of heat: Similar to what is done with electrons (known as “electronics”), the field of “heattronics” or “phononics” is emerging as an exciting nanotechnology development. The second reason is that it is directly related to one of the most basic questions of heat transport science—the validity of Fourier’s law.
Fourier’s law states that when energy flows between two heat baths at different temperatures, there is a well-defined temperature gradient and a constant thermal conductivity. While very successful from the engineering point of view, there is no microscopic derivation of Fourier’s law, except from trivial cases, and no general understanding as to when it breaks down. In fact, this long-standing open question was one of the driving forces for the development of numerical computations, beginning with the famous numerical experiment of Fermi, Pasta and Ulam at Los Alamos National Laboratory. Amazingly, more than half a decade after Fermi-Pata-Ulam, there are still many questions regarding Fourier’s law that are left unanswered, even very basic questions like the role of non-linearity and dimensionality in establishing Fourier’s law.
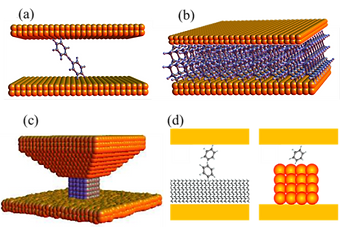
Fig. 1: Schematic depiction of some of the types of nano-scale junctions studied in my group: (a) single molecule junction, (b) molecular layer junction, (c) nano-particle junction, and (d) hybrid junctions.
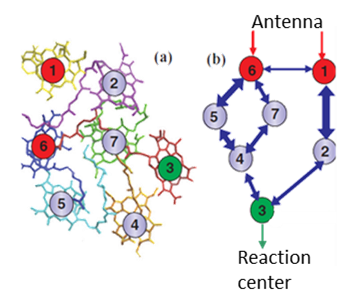
Fig. 3: (a) spatial structure of the photosynthetic complex subunit of green sulfur algae. (b) Effective network structure of the subunit. [Image adapted from Ai & Zhu, PRE 86, 61917 (2012)]
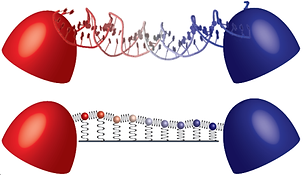
Fig. 4: Graphical depiction of the models for DNA, mapping the full DNA and environment with all its complex interactions onto a balls and nonlinear springs model.